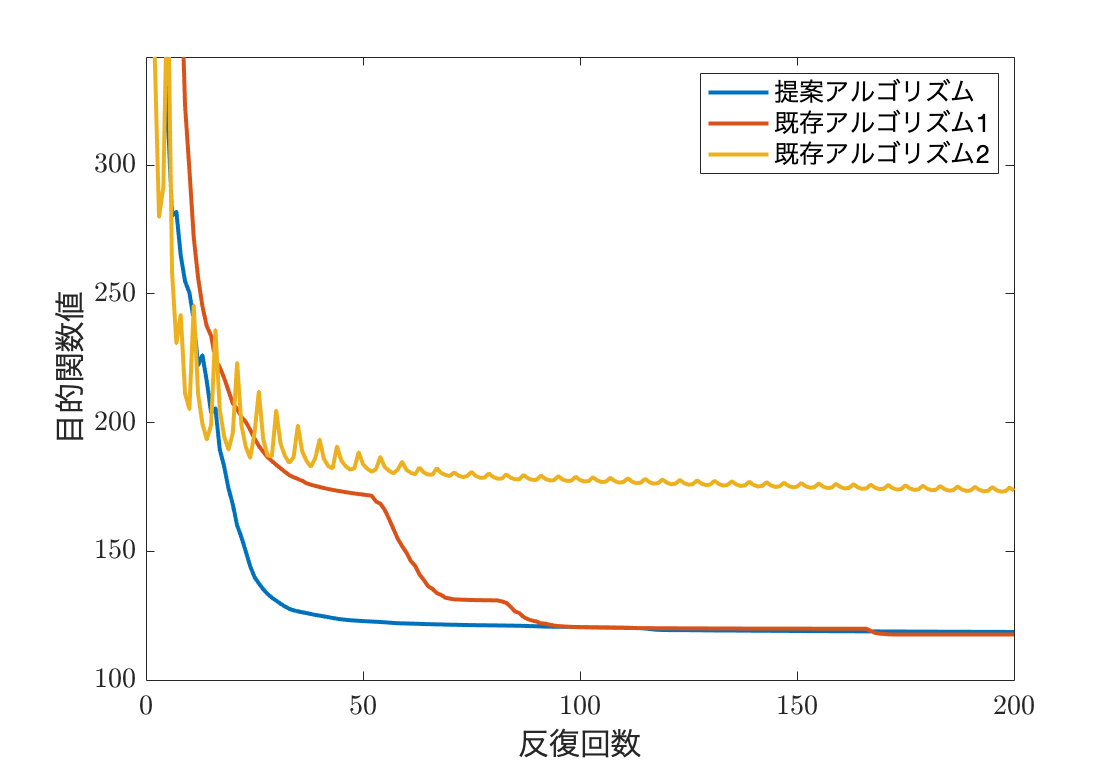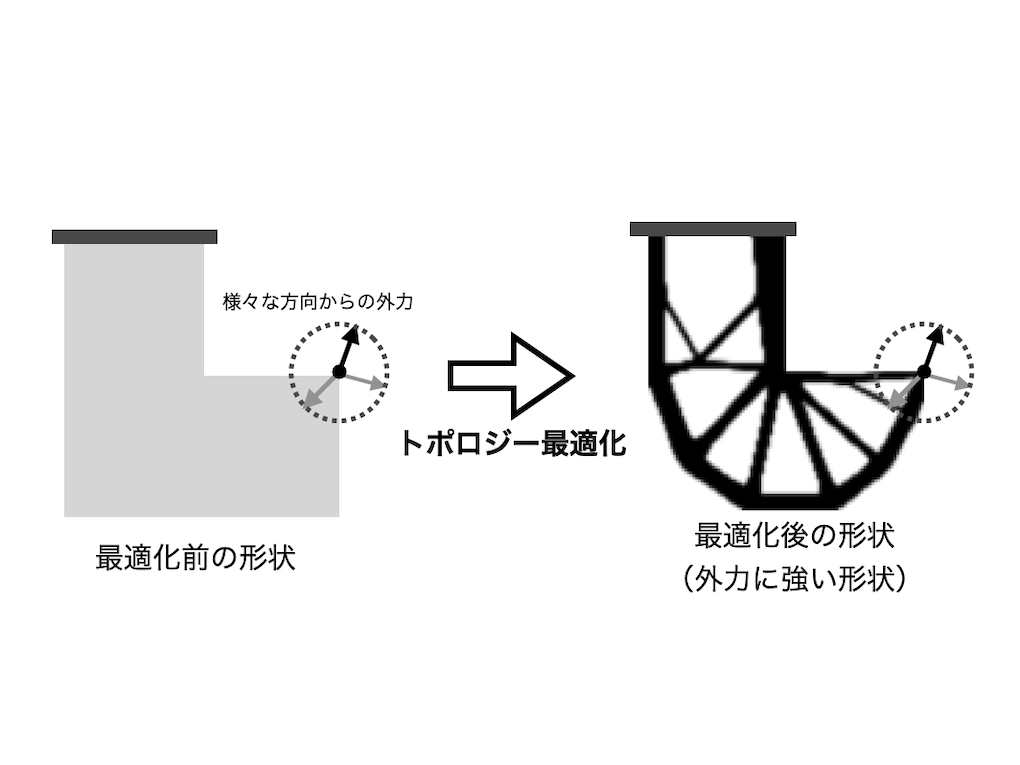
Research Key word: #Topology optimization #Optimization algorithm #Design engineering 1. Overview of the research This research proposes a method to optimize the design of structures by considering load uncertainties. For example, when designing a bridge, it involves considering safety during the design phase to ensure it doesn't collapse under unexpected heavy trucks. 2. The problem addressed: The research addresses the problem of minimizing the worst-case performance (e.g., maximum deformation) of structures under load uncertainty. Mathematically, this is formulated as a problem of minimizing the maximum eigenvalue, which is a non-smooth optimization problem (involving non-differentiable functions) that is challenging to solve. 3. Research motivation and background: In real-world engineering, it is crucial to design structures considering load uncertainties. Traditional solutions for such design problems faced challenges like high computational costs or lack of guaranteed convergence to optimal solutions. 4. Results obtained: A new algorithm was developed using a method to smoothly approximate non-smooth functions (smoothing method), ensuring convergence to optimal solutions. Numerical experiments showed that the proposed method converges to optimal solutions more quickly and stably than existing methods. 5. Relationship with value exchange (analysis/creation) and the potential impact of that research on society: This research contributes to creating and maximizing value through optimal design by enhancing safety, speeding up the design process, efficiently utilizing resources, and improving the reliability of structures. For example, being able to design social infrastructure like bridges and buildings more quickly, safely, and with fewer resources can lead to better infrastructure development and reduced disaster damage. Additionally, reducing material waste contributes to the realization of a sustainable society.
研究キーワード:#トポロジー最適化 #最適化アルゴリズム #設計工学 1. 研究の概要 この研究では、構造物の設計を荷重の不確実性を考慮して最適化する方法を提案しています。例えば、橋を設計する際に想定外の重いトラックが通っても壊れないように、設計の段階で安全性を考慮するというような事です。 2. 取り組んだ問題 荷重の不確かさがある状況下で、構造物の最も悪い状態での性能(例えば、最大の変形)を最小化するという問題を扱っています。この問題は数学的には、最大固有値を最小化する問題として定式化され、最適化計算が難しい非平滑な問題(微分できない関数を含む問題)となります。 3. 研究のモチベーションと背景 現実世界の工学では、荷重の不確実性を考慮した設計が重要です。このような設計問題に対する従来の解法では計算コストが高かったり、最適解への収束が保証されていなかったりという課題がありました。 4. 得られた結果 非平滑な関数を滑らかに近似する手法(平滑化法)を用いて最適解への収束が保証された新しいアルゴリズムを開発しました。数値実験では、提案手法が既存の手法よりも高速かつ安定に最適解に収束することを示しました。 5. 価値交換(または分析・生成)との関わりと、研究が社会に与えうるインパクト この研究は最適な設計を通して、安全性の向上、設計プロセスの迅速化、資源の有効活用、構造物の信頼性の向上などといった価値の生成、最大化に寄与しています。例えば、橋や建物など社会インフラの設計がより早く、安全に、少ない資源でできることは、社会インフラの整備や災害被害の軽減につながる可能性があるほか、材料の無駄を減らせることは、持続可能な社会の実現にも貢献します
PUBLICATIONS
- Akatsuki Nishioka, Yoshihiro Kanno, Smoothing inertial method for worst-case robust topology optimization under load uncertainty, Structural and Multidisciplinary Optimization, Vol. 66, No. 82, 2023/03
- Atsushi Maruyama, Maria Larsson, I-chao Shen, Takeo Igarashi, Designing Reconfigurable Joints, SIGGRAPH Asia, Technical Communications (SA '24), Association for Computing Machinery, Article No.: 34, Pages 1 - 4, New York, USA, 2024/12