
Focusing on “Researchers’ Big Picture,” this series explores the future societies they envision through their research. How does their research intersect with our lives? Their visions might provide valuable insight into the path ahead for all of us.
It is said that the processes behind human decision-making and behavior can be explained using algorithms. We asked Prof. Kawase, a researcher in algorithms, to elaborate on what this exactly means.

Interviewing:
・Name: Yasushi Kawase
・Affiliation: Project Associate Professor, Department of Mathematical Informatics, Graduate School of Information Science and Technology, The University of Tokyo
What exactly is an algorithm?
_______________________________
▶︎ The term “algorithm” is often heard but feels unfamiliar, carrying the impression of an unknown world. What is an algorithm?
An algorithm is a set of step-by-step instructions for solving a problem or performing a task efficiently. Algorithms are applied in many aspects of daily life. For example, when you type on a computer, predictive conversion candidates appear. Japanese has many homonyms. When you type “kaki,” the system predicts whether you mean kaki for “persimmon (fruit)”, “oyster”, or “summer season” based on previous input, and determines the order in which to display the candidates—that process involves an algorithm.
▶︎ Computers learn from the conversion results and the words adopted. Does the algorithm rewrite the learned results every time?
There are various ways to determine how candidates are displayed. Should it prioritize words that have been converted the most frequently in the past, or those converted most recently? For example, during summer, “summer season” might have been prioritized because it was converted more often, but when autumn arrives, “persimmon” increases, so the system prioritizes “persimmon.” This dynamic decision-making is also managed by an algorithm. All processes of decision-making that occur within a computer involve an algorithm. Furthermore, in automated stock trading systems, traders must instantly decide “when to sell and when to buy” based on constantly changing information. Algorithms are also used in such uncertain situations to aim for the optimal cumulative profit.
▶︎ So, the decision-making process itself is an algorithm. Therefore, it is fair to say that algorithms are closely related to daily life.
Yes. It can be said that algorithms are involved in every action within a computer. The display results might differ depending on the software or app used; this difference is due to the particular algorithm and the data being processed.
The world is driven by algorithms.
_______________________________
▶︎ Listening to you, I feel that algorithms are much more relatable. But your research is not on predictive conversion, is it?
I research a field called “Mathematical optimization”. Simply put, it is a mathematical method for finding the best possible result within a given set of constraints.
For example, when a store manager orders inventory, instead of deciding the quantity based on intuition or experience, mathematical optimization involves formulating various information (like season, weather, and warehouse space) into mathematical expressions and solving them using a computer to maximize profit. This reduces overstocking or stockouts, enabling efficient ordering.
Mathematical optimization includes various subfields. Finding the single most efficient route to visit all destinations in a day—where all necessary information is available beforehand to find the optimal solution—is called “Offline optimization”.
Also, when making the best decision at a given moment while information is changing in real-time—for example, in a taxi dispatch system where ride requests are constantly arriving, and the system must decide which taxi to assign to which user—this is called “Online optimization”. Within online optimization, there is a field called the “optimal stopping problem”, which researches at what point in time a decision should be made to increase the probability of a good outcome. This area includes famous examples like the “Secretary Problem” (or the Marriage Problem).
▶︎ That is an interesting name. I am curious about the Secretary Problem. What exactly is it? It sounds related to business.
The Secretary Problem is the question of how to maximize the probability of hiring the best candidate when interviewing candidates sequentially, one at a time. It is said to be useful in business decision-making. The rule is that you must decide whether to hire the candidate immediately after their interview.
Let’s try a quick demonstration. In real life, you would only know each person’s evaluation score during the interview but here I will show all scores at once for simplicity.
Let’s begin. The first candidate has arrived. Their score is 2025. Will you hire them?

▶︎ I will wait and not hire yet.
That is reasonable. Since there are 10 candidates, you don’t know but the following candidates could be better. So, generally, waiting and observing is the better strategy.
The second candidate has arrived. Their score is 1521. Although the scores might continue to decline, since it’s only the second candidate, the probability of a better person coming later seems to be still high, so you decide not to hire.
The third candidate’s score is 2704. This is the best score so far. What do you do? Will you hire this person?
▶︎ I see, so the goal is to find the strategy that maximizes the probability of hiring the best person. But can this actually be calculated?
Math can be used to determine how to increase its probability. In the Secretary Problem, there is the “37% Rule”, which states that the probability of making the best selection is maximized if you wait for the first 37% of candidates to pass before making a decision. This rule is often used as a reference point in actual decision-making scenarios.
秘書問題_河瀬-1200x675.jpg)
▶︎ I haven’t hired anyone, so I’m not familiar with that scenario. Could you explain it with another relatable example?
Have you ever driven to a crowded shopping center parking lot, where only a few spots are available, wanting to park as close to the entrance as possible, but after hesitating, you end up parking far away from your desired spot?
The optimal stopping problem can be applied here to determine the best time to commit to a parking spot. The key is to set a constraint, such as deciding to park within 10 minutes or within 10 space candidates. Once you set that limit, you first passively observe the initial 37% of potential spots. You note the best spot found during this observation period. After the 37% observation period, the moment you find a spot that is better than the one you remember, you take it. This strategy increases your chance of getting a near-optimal spot.
The 37% rule can also be applied when you want to book a flight or a bullet train ticket, or when you are gauging the optimal timing to buy a house.
▶︎ Since I have personally experienced the frustration of making bad decisions, like with parking or ticket booking, I am surprised to learn that there is such a close connection between human behavior and algorithms, and that utilizing algorithms effectively can lead to life hacks.
Move back and forth between theory and Implementation to Find the Best Solution
_______________________________
▶︎ I assume you design algorithms to suit each specific problem. What is your general workflow for proceeding with a project?
Let’s use the example of driving from Tokyo Station to Tsutenkaku Tower in Osaka. First, we define the evaluation metric for the problem. While various goals exist—such as getting there fast, cheaply, or via the shortest route—here we decide on “shortest distance” as the metric. Next, we perform modeling. Modeling is the process of extracting the essence from the real world and re-expressing it in the theoretical domain.
For example, we extract information on the “locations (nodes)” (Green circle in a picture below) such as intersections and junctions between Tokyo and Osaka, and the “road segments (links)”(gray lines in a picture below) that connect them, along with the distance information for each segment. We then use this information to search for a route from the Tokyo Station node to the Tsutenkaku Tower node. The length of the route is defined as the sum of the distances of all traversed segments (links). In this way, the problem is modeled as an optimization problem: “Which route yields the minimum total distance?”
ノードとリンク.png)
②Since the number of possible routes is vast, checking every single route is challenging even with a computer. However, by using an appropriate algorithm, the problem can be solved.
Once the model is complete, the optimal route (solution) is derived by feeding the extracted information into the algorithm.
実社会と理論04-1200x716.jpg)
▶︎ Why is it necessary to first move from the real-world problem into the theoretical domain?
Passing through the theoretical domain allows us to extract only the essence of the problem, leading to more versatile solutions. With the Secretary Problem, for example, we were able to apply the same model to not just hiring, but also to timing parking or making reservations. Similarly, in the shortest path problem, although we initially considered distance, the same modeling and algorithm can be used to solve for minimum travel time or minimum cost.
However, extracting the essence alone does not guarantee a solution to the real-world problem.
▶︎ What do you mean by that?
Let’s use the example of a meal. If you try to optimize what food to buy to meet nutritional requirements while minimizing cost, the optimal solution might simply be to buy only rice and cabbage.
▶︎ Really? While that might be efficient…
Yes, the question would be, can you actually live on just rice and cabbage?
As this shows, when we model a problem and extract only the bare essence, the resulting solution can sometimes be incompatible with the real world. If we consider a meal to include not just the nutrients required for survival, but also taste, appearance, etc., then a model that only considers nutrition and cost is incorrect.
When these shortcomings become apparent, we update the model by adding new constraints – such as incorporating variety or appearance. By repeating this process of trial and error, we move toward a complete solution.
-1200x675.png)
▶︎ So, it’s not a single”one-shot answer,” but a process of repeatedly seeking the best solution. I didn’t know that.
Initially, if you ask “What food meets nutritional requirements without spending much money?”, immediate answer might be something that is simply nutritionally efficient. It’s important to first solve it based on a model that reflects that initial, simple understanding. Otherwise, you cannot determine what is truly essential and what can be omitted. That is why the process involves finding a solution based on the bare essence first, and then improving upon it.
▶︎ I see. Are you involved in all areas shown in the previous diagram?
Yes. Although my main research is on the algorithms within this theoretical domain, I am involved in all parts of the process as the other steps are necessary components of the work. Being said that, personally, I am fascinated by the simple, theoretical domain where we can focus solely on the essence of a problem.
▶︎ So, you are constantly working with mathematical formulas, searching for better algorithms?
While developing the best possible algorithm is certainly part of the job, I also work on proving that no better solution exists than the current one. For instance, various algorithms can be conceived for the Secretary Problem, but it has been proven that no algorithm can achieve a success rate better than 37%.
Therefore, my work involves both creating new algorithms and finding the limits of existing algorithms. Actually, proving something is “the best” is quite difficult. To prove something is not the best, you just need to bring a better option. But to prove something is the best, you must show that any alternative is inferior. It is quite a challenging field.

Bringing Timely Value to Society with Algorithms
_______________________________
▶︎ Listening to the various examples, now I know that algorithms have a big impact on society.
That is correct. In terms of societal applications, algorithms are used, for example, to determine the optimal placement of refugees fleeing conflict zones into various refugee camps, considering capacity and other conditions (a field known as “Stable Matching”).
They are also used to reduce traffic congestion by adjusting the timing of traffic lights based on seasonal traffic volume predictions, and in production planning to minimize the total cost of manufacturing and transportation—by determining how much product to manufacture and how much inventory to hold in which warehouses.
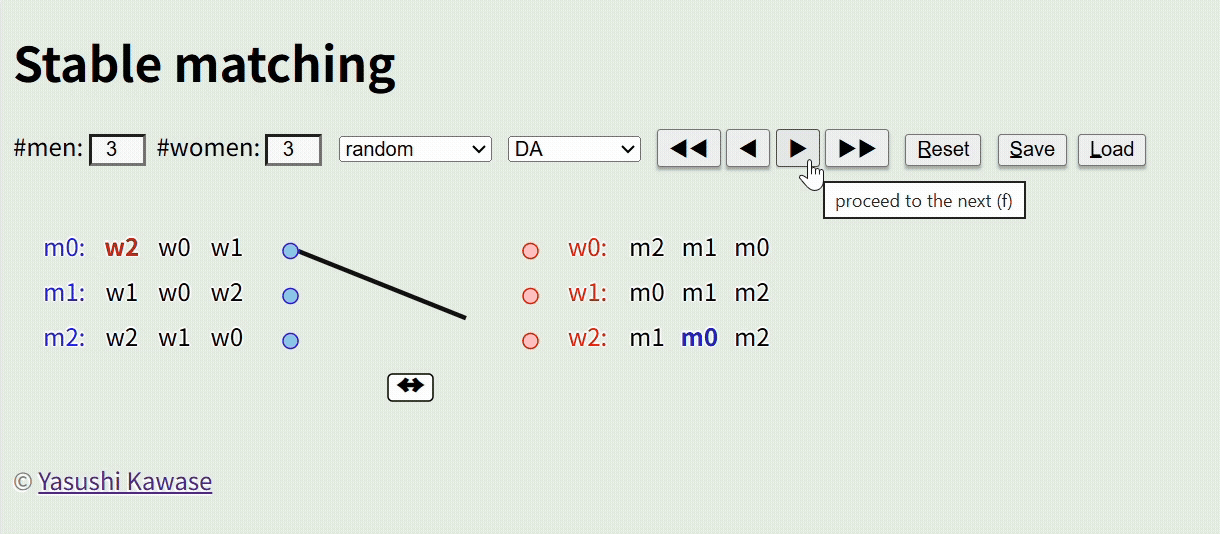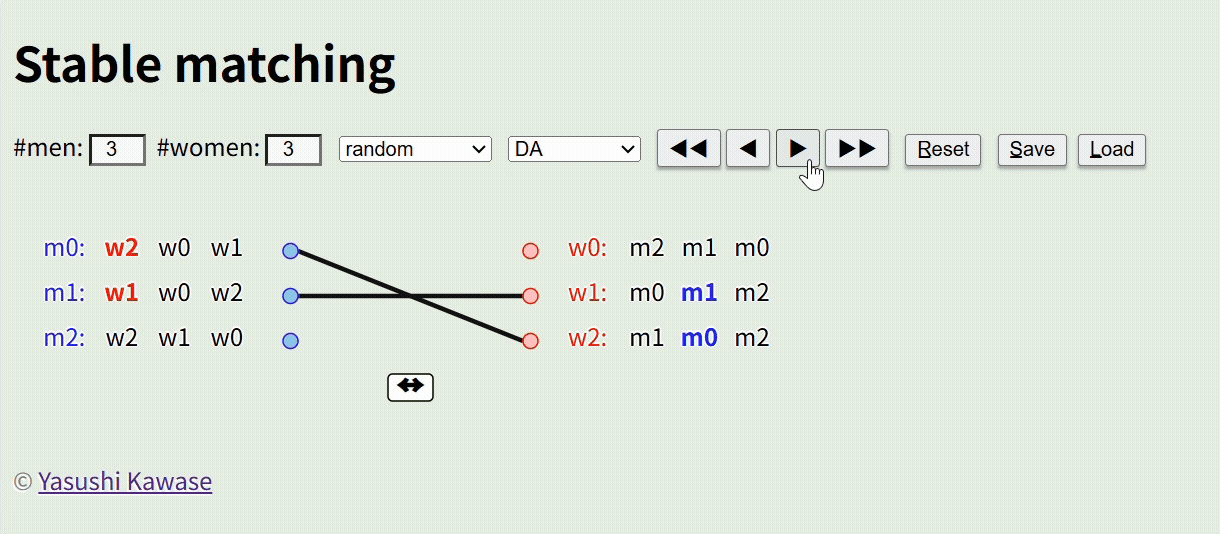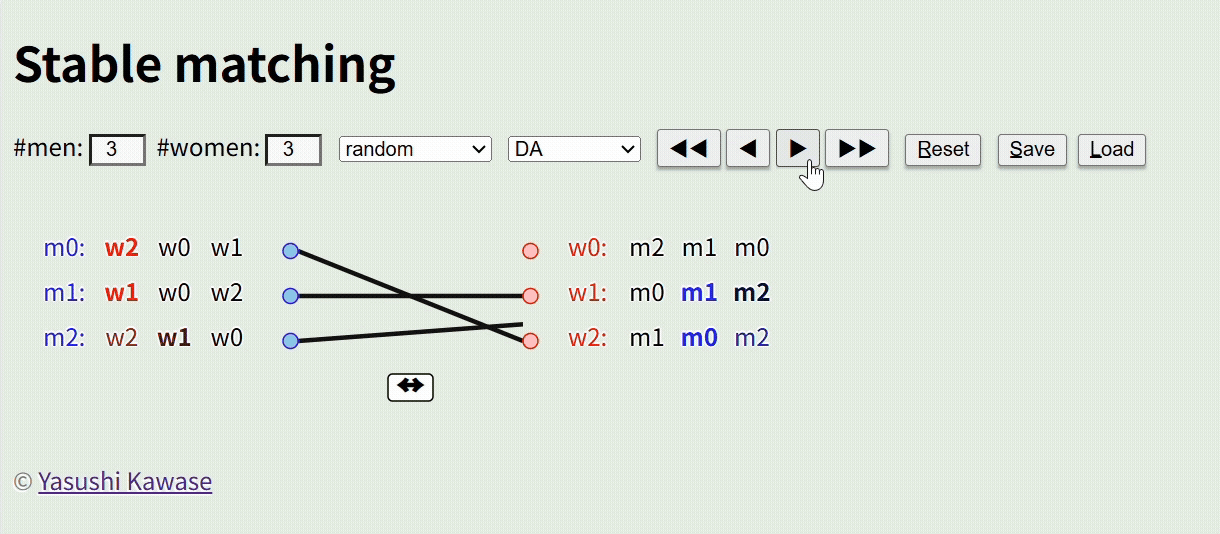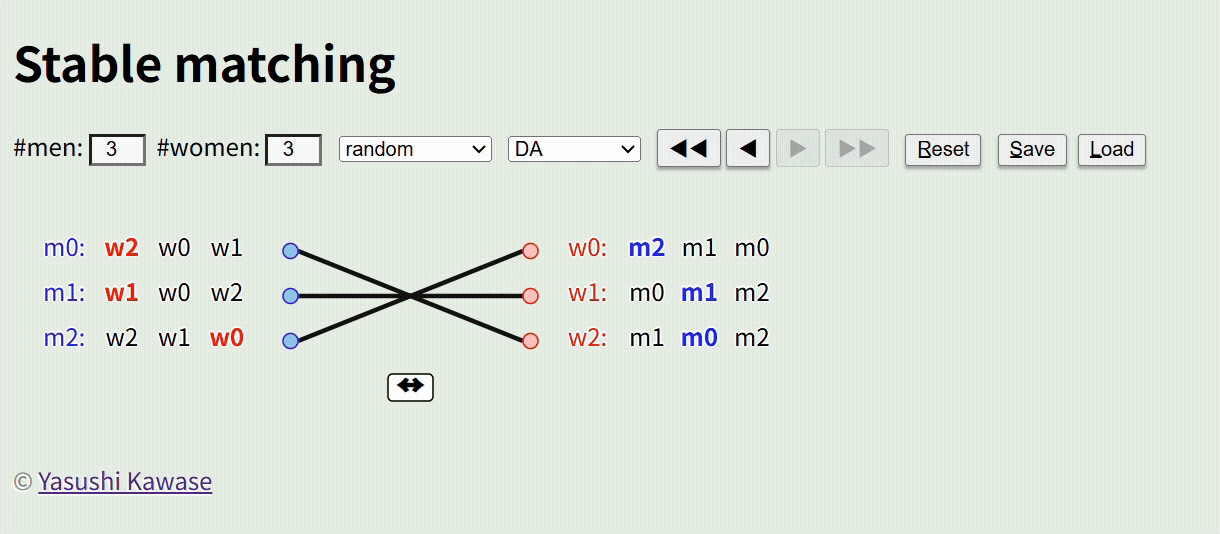
Imagine a scenario with three men (m0, m1, m2) and three women (w0, w1, w2), where the preferences of each person have been collected (e.g., m0 prefers w2>w0>w1). The goal is to create pairs that satisfy everyone’s preferences as closely as possible. Even with just three people, preferences may clash, requiring multiple re-dos.
When the number of participants grows to dozens or thousands, human decision-making becomes impractical. Solving this mathematically is the domain of “Stable Matching”.
This method is widely used, for example, in assigning medical residents to hospitals.
▶︎ So, algorithms are involved not only in everyday problems but also in social and global issues. How are you currently applying your research back to society?
Public awareness is shifting toward sustainable societies and ethical consumption, leading to increased interest in the secondhand market, including platforms like Mercari. (Japanese online C2C flea market app) Manufacturers are also paying attention to this shift, and I also assist them in examining whether they should enter the certified refurbished market.
Specifically, I use mathematical optimization to analyze complex consumer decisions: If the same item is available both new and certified refurbished, which will the buyer choose, and what decision-making process led to that purchase? I also analyze how selling prices are determined in the secondhand market. This reveals the market conditions under which a manufacturer should enter the certified refurbished market and whether that move will ultimately contribute to promoting the circular economy.(Referece: 「サーキュラーエコノミーを語る」〜ゲーム理論で解く!メーカーの認定中古品がもたらす経済・環境的インパクト~)
Furthermore, on platforms like Mercari, we can provide buyers with “optimal timing” suggestions—for example, advising whether they should buy now even if the price is a bit high, or wait because the price is likely to drop soon.
By vitalizing the secondhand market in ways that satisfy both sellers and buyers, we believe we can actively promote a sustainable society.
▶︎ From the perspective of “a future where fair and safe value exchange can take place,” which the Value Exchange Engineering initiative advocates, what do you envision for the future based on your research?
The application of optimization leads to the creation of a social system where “necessary resources are delivered to the right place, at the right time, in the right quantity.” This not only reduces waste and allows us to effectively use limited resources but also makes it possible to introduce fairness into the distribution of resources and services.
Taking human resources as an example, efficiency could ensure “Right person in the right place”, providing equal opportunities for everyone to utilize their abilities. I believe this can contribute to realizing a fair society where the value of resources, including people and goods, is maximized in fields like business, medicine, and welfare, and everyone can benefit equitably.
▶︎ Hearing till now, I believe people would want to consult with you when they face an issue, whether it’s reviewing costs, improving efficiency, or addressing HR problems. Could you tell us how much and what we should prepare when we consult with you?
For initial discussion, the issue you want to solve, rough idea of how to evaluate the result, necessary constraints and the variables would be enough.
For example:
- Problem: Efficiently distribute newsletter that interests each user
- Evaluation Metric: Number of user clicks
- Necessary Constraints: (1) Type A newsletter must always be sent (2) The total number of newsletter sent to one person must be within XX(quantity) per week
- Variables: Which email to send to which user
After that, we will work together to refine the constraints and metrics to create the mathematical model. Then we design the algorithm. Since the ideal solution rarely appears on the first try, we run an initial test. This trial helps reveal factors missing from the objective function—like, “Oh, we needed this too.” We can then add those defined conditions and solve the problem again, iteratively optimizing the solution.
▶︎ I felt that Prof. Kawase’s research leads toward a future that is kind to all people—a fair society where mistakes due to poor choices are minimized, recovery is quick, and solutions are agreeable to everyone. Although I don’t understand the formulas, I feel closer to the math that works behind the scenes in our daily lives.I asked him one final question: “What is the appeal of mathematics?” Prof. Kawase responded, “Because mathematics deals only with the essence of things, detached from real-world constraints, mathematically beautiful concepts are expressed very simply. There is a puzzle-solving enjoyment in continuously pushing for that simplicity.” This made me realize that seemingly complex everyday phenomena are merely simple at their core principles, and the key is discerning that essence. This insight is also applicable to the worlds of management and design etc.,
Algorithms will undoubtedly become even more integrated into our lives. I would be excited to follow how they transform society and our daily experiences.
Kawanaka, VXE Outreach team
Related link
・Yasushi Kawase